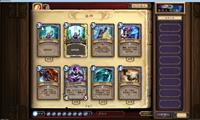
T2賊相信不少玩家都聽說過吧, T2賊指的不是T2強度的盜賊卡組, 而是和T7獵類似的在第二回合就能夠結束戰鬥的卡組, 聽上去是不是很不可思議?來看看卡組就知道是怎麼回事了!

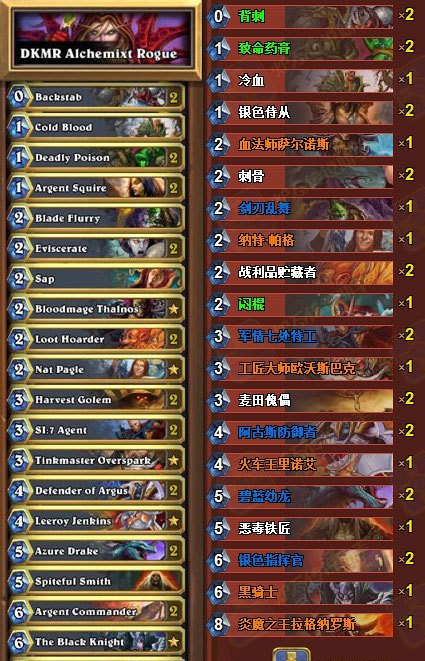
(上圖為以前版本的T2賊, 現在版本的賊, 但是核心卡牌沒有改變, 屬於用過的最經典版本。 現在版本也就替換一些退環境了的卡牌, 實際上無關緊要, 貓頭鷹繼續帶一張)
T2賊後手1費龍鷹, 只要對面不解, 2費, 硬幣, 冷血, 冷血, 叫囂, 暗影步, 叫囂, 暗影步, 叫囂=30血!
這應該是爐石傳說最快的一套。 達成條件比較苛刻。
我知道大家不信我, 所以我發個計算過程的一部分, 最近考試比較忙, 所以沒辦法驗算和講解, 下面簡單講解一下這個過程。
十萬分之六是指0.00006, 不是準確值, 後面還有小數。 當然準確值是個分數, 我最近沒有時間, 所以沒有算。 總之不能約分成五萬分之三。
粗略估算的話數量級是4/(30C6),
30張牌, 不算幸運幣的話, 一費回合需要一張龍鷹, 簡記為“龍”, 二費回合需要一張叫囂, 簡記為“叫”, 兩張冷血, 兩張暗影步, 這四顆法術可以簡稱四“法”。 其他無關的有22張牌, 簡記為“其”。
這個問題最噁心的地方在於起手的四張手牌是可以換的, 而如何換牌能使天胡概率最大也是未知的, 所以不妨先考慮換牌之後的情況。
換完牌之後的手牌能得到天胡的有四種情況:a.四法, b.三法龍, c.三法叫, d.二法龍叫, 先求出abcd對應的天胡的條件概率。
現在考慮換牌前的起始手牌, 剛好共有26種情況(剛好用英文字母表示), 計算每種情況出現的概率, 再考慮每種情況換牌後出現abcd這四種情況的概率,
發一些具體過程。
換完牌之後的手牌情況有很多, 但能得到天胡的只有四種情況:a.四法, b.三法龍, c.三法叫, d.二法龍叫。
不妨假設我們已經得到了情況a, 設此時天胡的概率為Pa(有高中知識的人應該知道這是條件概率)。
首先我們一費摸牌時必須上手一張龍, 牌堆裡現在有26張牌, 龍在牌堆裡有兩張, 所以這一步概率是2/26, 二費時我們必須上手一張叫囂, 概率是2/25。
所以Pa=(2*2)/(26*25)=2/325
同樣地, 我們計算Pb=2/325, Pc=1/325, Pd=1/325。
最輕鬆的部分完成。
為了書寫方便, 我們把Pa記作a。
現在考慮換牌之前的26種情況。
A.其*4, 其出現概率是4C22/4C30, 換牌策略是全換, 全換之後有1/26C4出現情況a, 8/26C4出現b, 8/26C4出現c, 24/26C4出現d, 所以是(a+8b+8c+24d)/26C4。
依此類推
B.其3龍1, 出現概率是2*(22C4)/4C30, 換牌策略是換掉其3, (4*b+12*d)/26C3。
C.其3叫1, 出現概率是2*(22C4)/4C30, 換牌策略是換掉其3, (4*c+12*d)/26C3。
D.其3法1, 出現概率是4*(22C4)/4C30, 換牌策略是換掉其3, (a+6b+6c+12d)/26C3。
為了書寫方便, 更換書寫格式。
例如:
A.其*4, 其出現概率是4C22/4C30, 換牌策略是全換, 全換之後有1/26C4出現情況a, 8/26C4出現b, 8/26C4出現c, 24/26C4出現d, 所以是(a+8b+8c+24d)/26C4。
寫作:
A.其4, 4C22/4C30, 換其4, (a+8b+8c+24d)/26C4。
下面繼續補充各種情況:
E.其2法2,
F.其2法1龍1, 8*(2C22)/4C30, 換其2, (3b+6d)/26C2。
G.其2法1叫1, 8*(2C22)/4C30, 換其2, (3c+6d)/26C2。
H.其2龍2, 2C22/4C30, 換其2龍1, (3b+12d)/26C3。
I.其2叫2, 2C22/4C30, 換其2叫, (3c+12d)/26C3。
J.其2龍1叫1, 4*(2C22)/4C30, 換其2, (6d)/26C2。
K.其1法3, 4*22/4C30, 換其1, (a+2b+2c)/26。
L.其1法2龍1, 12*22/4C30, 換其1, (2b+2d)/26。
M.其1法2叫1, 12*22/4C30, 換其1, (2c+2d)/26。
N.其1法1龍2, 4*22/4C30, 換其1龍1, (3b+6d)/26C2。
O.其1法1叫2, 4*22/4C30, 換其1叫1, (3c+6d)/26C2。
P.其1法1龍1叫1, 16*22/4C30, 換其1, 3d/26。
Q.其1龍2叫1, 2*22/4C30, 換其1龍1, 6d/26C2。
R.其1龍1叫2, 2*22/4C30, 換其1叫1, 6d/26C2。
S.法4, 1/4C30, 不換, a。
T.法3龍1, 8/4C30, 不換, b。
U.法3叫1, 8/4C30, 不換, c。
V.法2龍2, 6/4C30, 換龍1, (2b+2d)/26。
W.法2叫2, 6/4C30, 換叫2, (2c+2d)/26。
X.法2龍1叫1, 24/4C30, 不換, d。
Y.法1龍2叫1, 8/4C30, 換龍1, 3d/26。
Z.法1龍1叫2, 8/4C30, 換叫1, 3d/26。
下面就是最噁心的一步了, 驗證每一個資料計算是否正確, 然後把這些數乘起來, 再加起來, 再乘1/2(後手的概率)
我目前是沒有這個信心和勇氣的, 有興趣的小夥伴可以來嘗試下。